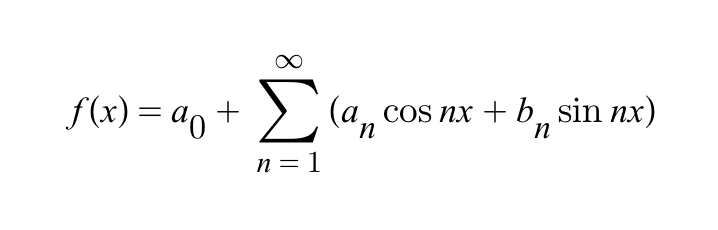삼각비를 처음 공부하는 방법_ 프톨레마이오스 삼각비1 워크북 작성
2024.07.25

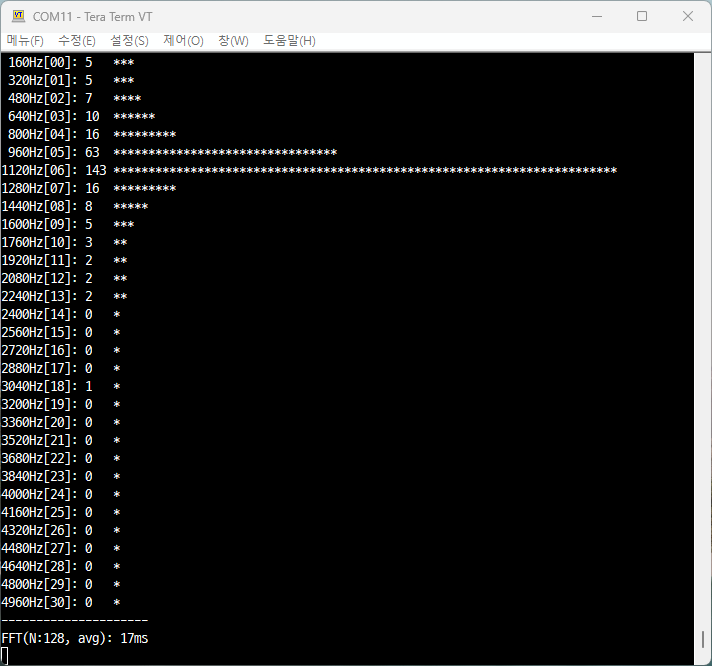
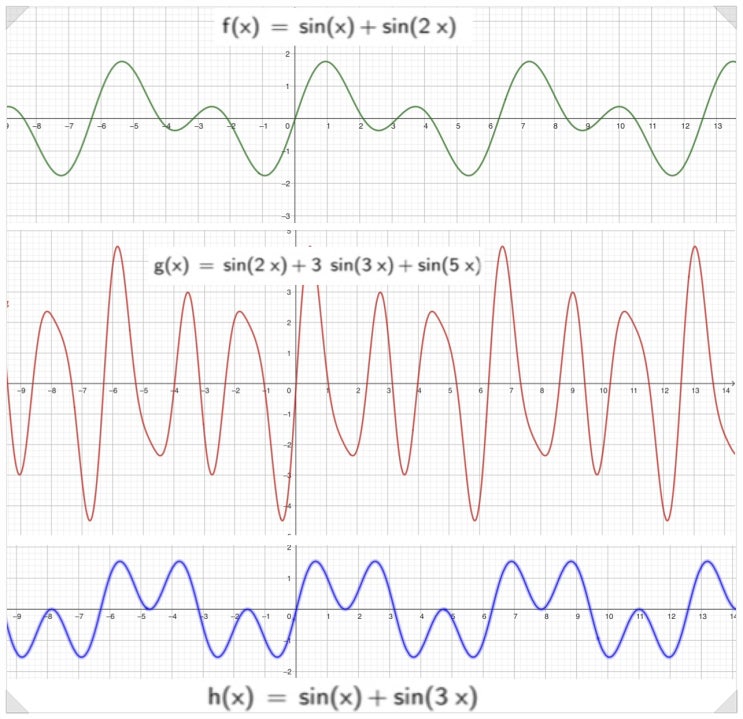
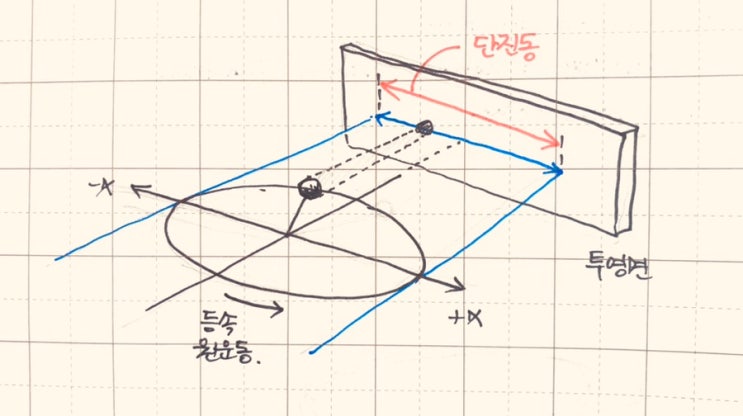
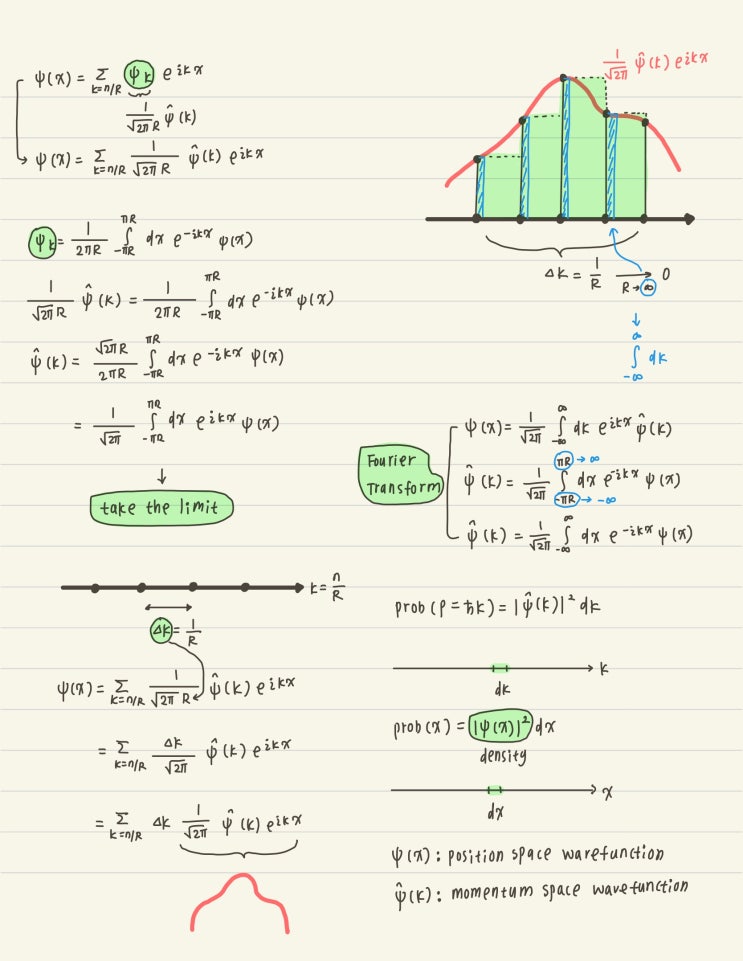
중3-2 수학교과에 처음 등장하는 삼각비는 일단 다양한 약속과 용어를 기호화하여 나와 학생들을 꽤나 힘들...
출처
https://blog.naver.com/crimsonrnemath/223198749429
이슈모어 핫이슈
관련 포스팅
Copyright blog.dowoo.me All right reserved.