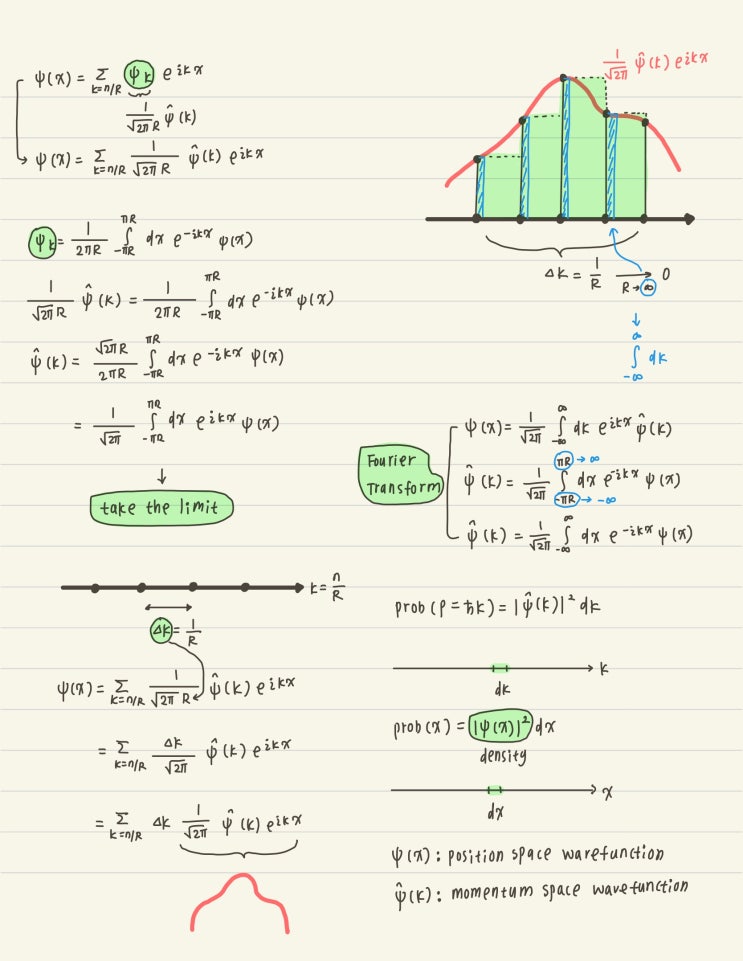
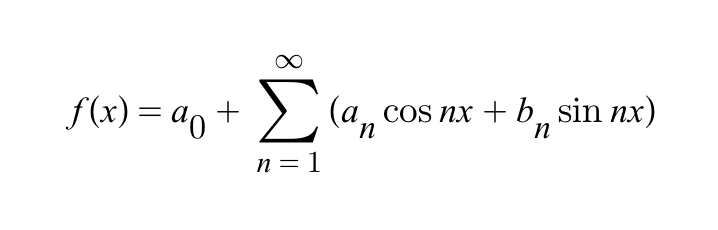푸리에급수로 향하는 주기함수의 조건을 찾기 1부.
2024.07.25

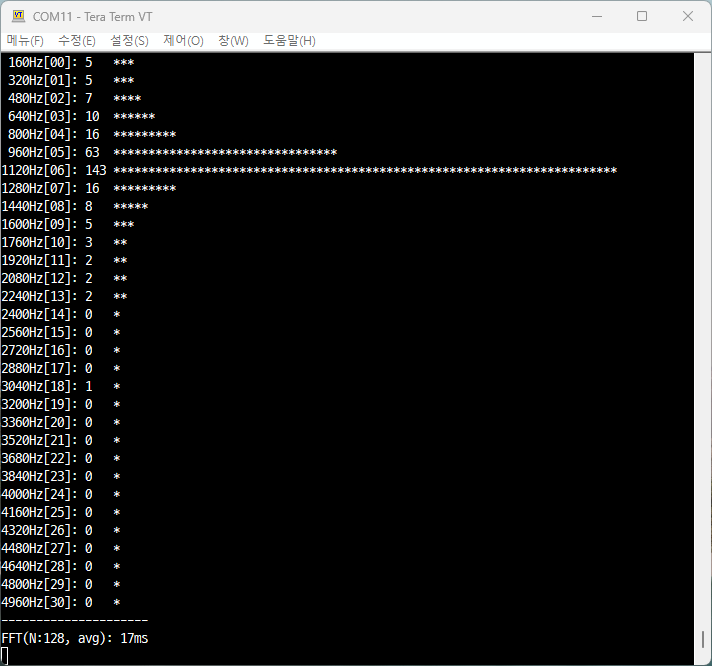
일단, 실용적으로 푸리에 급수가 2*pi 를 주기로 갖고 2번 미분가능하며 1,2 계 미분계수가 모든 실수 x 에...
출처
https://blog.naver.com/joungdongjin/223266692596
이슈모어 핫이슈
관련 포스팅
Copyright blog.dowoo.me All right reserved.