평택수학학원 본수학 수1 삼각함수와 실생활의 활용사례
2024.07.25
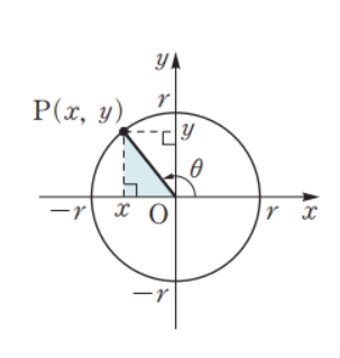
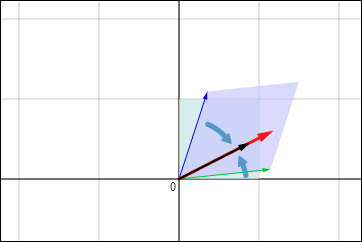
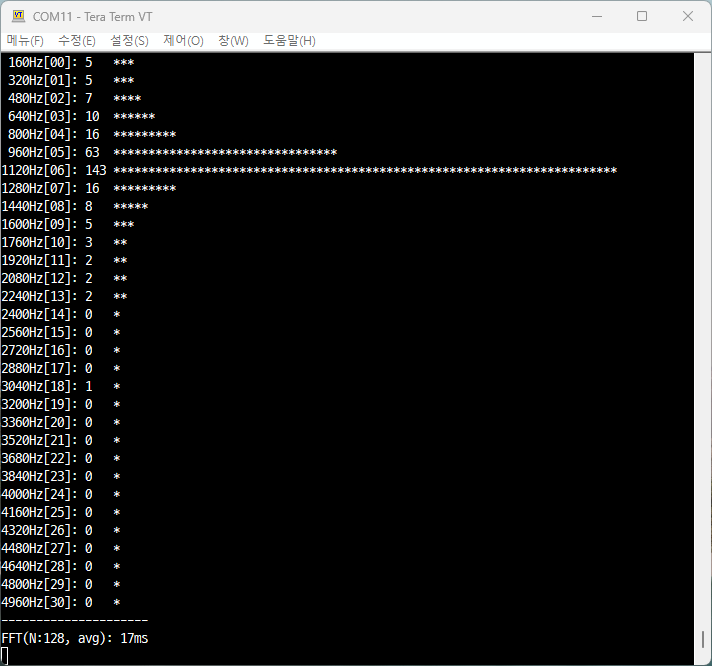
오늘은 고2 수1 수학 교과 과정의 삼각함수가 다양한 분야에서 활용되고 있는데, 실생활에서의 활용 사례와...
출처
https://blog.naver.com/bigdream003/223422335911
이슈모어 핫이슈
관련 포스팅
Copyright blog.dowoo.me All right reserved.